In the following we will give a short introduction into the theory of shearlets. The shearlet transform is unlike the traditional wavelet transform which does not posses the ability to detect directionality, since it is merely associated with two parameters, the scaling parameter a and the the translation parameter t. The idea now is to define a transform, which overcomes this vice, while retaining most aspects of the mathematical framework of wavelets, e.g., the fact that

• the associated system forms an affine system,
• the transform can be regarded as matrix coefficients of a unitary representation of a special group,
• there is an MRA-structure associated with the systems.

The shearlets satisfy all these properties in addition to showing optimal behavior with respect to the detection of directional information.

The basic idea for the definition of continuous shearlets is the usage of a 2-parameter dilation group, which consists of products of parabolic scaling matrices and shear matrices. Hence the continuous shearlets depend on three parameters, the scaling parameter a > 0, the shear parameter s ∈ R and the translation parameter t ∈ R², and they are defined by

ψ_a,s,t(x)=a^-3/4 ψ ((D_a,s^-1 (x-t)), where D_a,s = [a,-a^1/2s;0,a^1/2].

The mother shearlet function ψ is defined almost like a tensor product by

ψ(ξ₁,ξ₂) =ψ₁(ξ₁)ψ₂(ξ₂/ξ₁),

where ψ₁ is a wavelet and ψ₂ is a bump function. The figure on the right hand side illustrates the behavior of the continuous shearlets in frequency domain assuming that ψ₁ and ψ₂ are chosen to be compactly supported in frequency domain.

The associated continuous shearlet transform again depends on the scaling parameter a, the shear parameter s and the translation parameter t, and is defined by

SH_f(a,s,t) = <f,ψ_a,s,t>

This transform can also be regarded as matrix coefficients of the unitary representation

(σ(a,s,t)ψ)(x) = ψ_a,s,t(x)=a^-3/4 ψ ((D_a,s^-1 (x-t))

of the shearlet group S=R⁺ x R x R² with multiplication given by

(a,s,t) • (a',s',t') = (a a', s+s'a^1/2, t + D_a,s t').

The continuous shearlet transform precisely resolves the wavefront set, since the location parameter t does detect the location of singularities, whereas the shear parameter shows the direction perpendicular to the direction of the singularity.

To illustrate the ability of shearlets to detect directions, the following images show ψ_a,s,t in the time and frequency domain for a=0.3, s=0 and t=0.

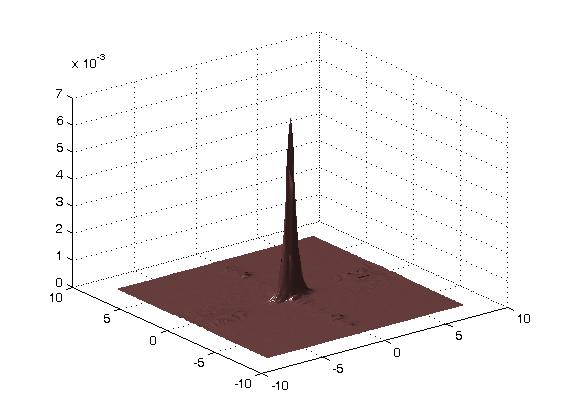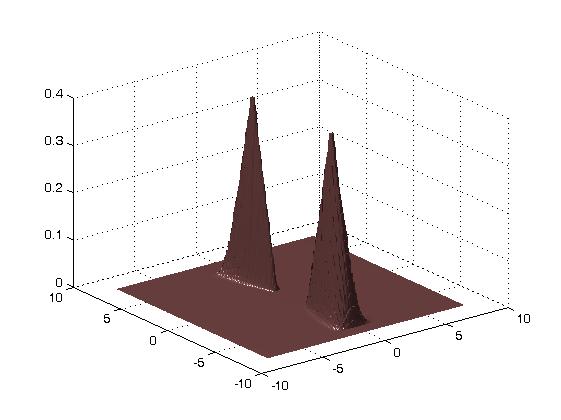The next images illustrate the behavior of shearlets with respect to the shearing operator. The image on the left-hand-side shows ψ_a,s,t for a=0.3, s=-0.5 and t=0, whereas the image on the right-hand-side shows its Fourier transform.

 

 

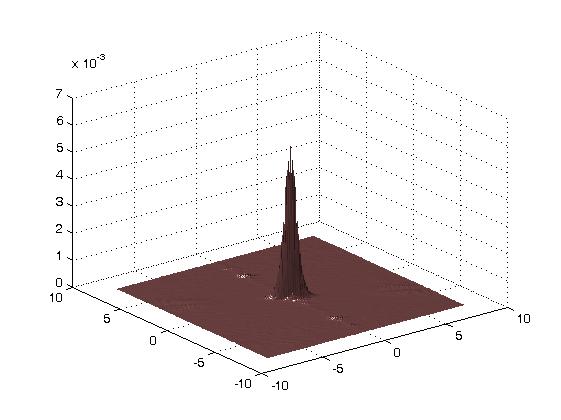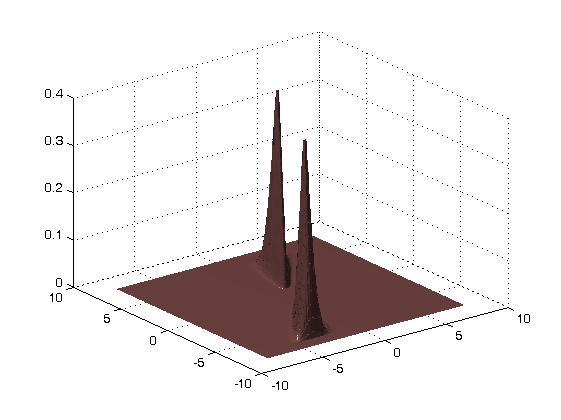The directionality of the shearlets in time domain is evident.

By sampling the continuous shearlet transform on an appropriate discrete set of the scaling, shear, and translation parameters, it is possible to obtain a frame or even a Parseval frame for L²(R). We will briefly discuss two possibilities to discretize the continuous shearlet transform.

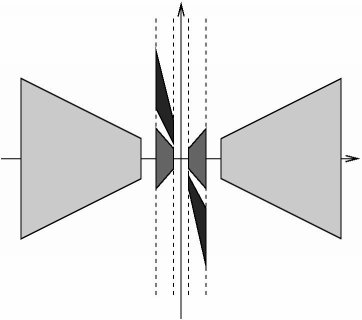
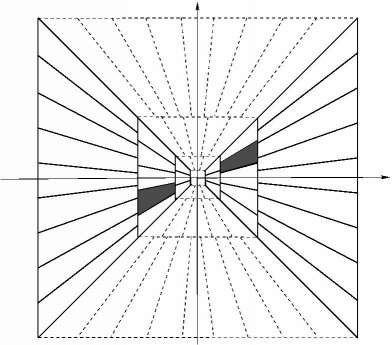
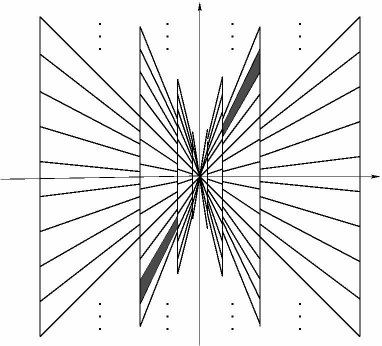
To obtain the discrete shearlets, we sample the three parameters as a_j=2^j (j ∈ Z) , s_j,k=k a_j^1/2 =k2^j/2 (k ∈ Z), and t_j,k,m=D_aj,sj,k (m ∈ Z²). We choose the mother shearlet function ψ in a similar fashion as in the continuous case, i.e., we now choose ψ₁ to be a discrete wavelet and ψ₂ to be bump function with certain weak additional properties. The tiling of the frequency plane is illustrated in the figure on the left hand side.

This system forms a Parseval frame for L²(R), and they are optimally sparse. Furthermore, they are associated with a generalized MRA-structure, where the scaling space is not only translation invariant but also invariant under the shear operator.