Applications

Below we present the work on various applications where shearlets are used. This includes results from the use of ShearLab as well as purely theoretical results. If you know of  an application that is not yet listed here and you feel it should, please feel free to contact us.

Deep microlocal reconstruction

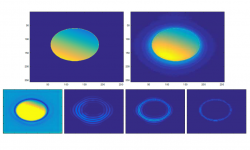
We propose a method that joint reconstruct images from tomographic data and reconstruct invisible singularities. 

 

External Links

Selected Papers

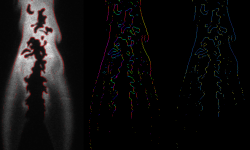
Learned wavefront set extraction and semantic edge detection

                     

                   

 

The study of oriented singularities plays an important role in different image processing tasks, in particular one can use it as a-priori information for inverse problems regularization in imaging, e.g. Computed Tomography. 

The wavefront set characterizes the singularities of a distribution and its orientations. The asymptotic analysis of the Shearlet coefficients can be used to compute the wavefront set, this property has been studied for different classes of shearlets, from the band limited [KL] to the compactly supported case [G] and [KP]

Using this principle, there are at hand different approaches to implement an edge and orientation detector using shearlets. A first successful approach was made by Yi et al. [YLEK]. Another approach proposed by Reisenhofer and King [RKK] makes use of a complex-valued shearlets and extends the detected singularities to ridges. 

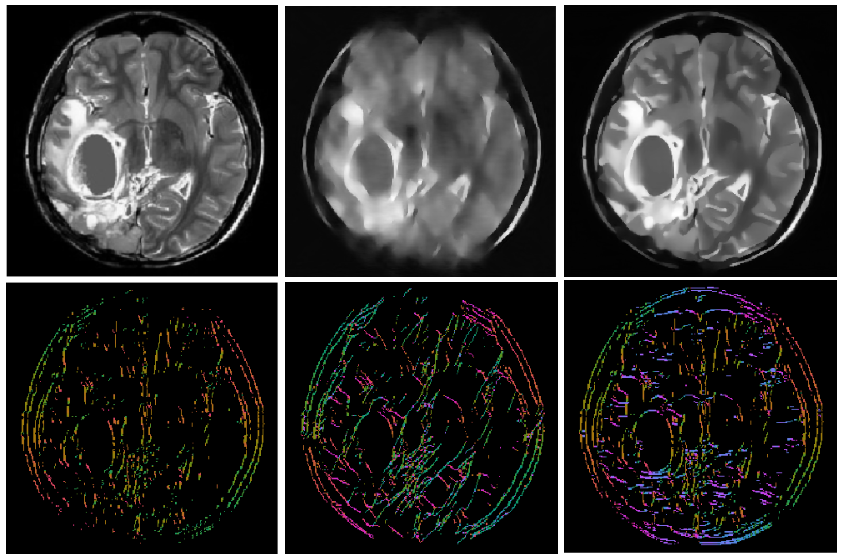
More recently, Andrade-Loarca et al. [AKOP] proposed a method that uses the optimal image representation provided by shearlets and the highly specialized and accurate classification capabilities given by deep neural networks to construct a digital wavefront set extractor named DeNSE (Deep Network Shearlet Edge Extractor). This method outperforms the previous existing methods and poses the capabilities to detect singularities with different degrees of regularity.

On the other hand, one can generalize the concept of edge detection and classification, to other classes, different from the orientations of the edges, this task is known as Semantic Edge Detection (SED). One can perform also high quality semantic edge detection by using existing deep learning approaches, but modifying the input to the shearlet coefficients, and reducing the buffer layers. The shearlet coefficients will perform the heavy lifting necessary so the removed buffer will not affect the performance. In fact Andrade-Loarca et al. [AKO] showed that this reduce the number of learnable parameters and augments the accuracy. 

External Links

  • Deep Network Shearlet Edge Extractor (DeNSE) Toolbox: A python toolbox that uses Shearlab.jl and tensorflow to extract the wavefront set of digital 2D images (and other kind of arrays) via shearlet image representation and deep neural networks-based classification. 
  • ShearSED: Shearlet Semantic Edge Detection Toolbox: A python toolbox that performs high quality semantic edge detection using Shearlab.jl, tensorflow and pytorch to extract the wavefront set of digital 2D images, using as base the CASENet and DDS architectures, modifying the input layer as the Shearlet transform and removing the buffer layer. 

Selected Papers

Edge and Ridge Detection and Analysis

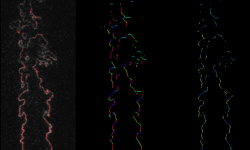
Many applications require the automated detection of features such as edges or ridges in images. Furthermore, geometric properties of these features like the local tangent orientation or the local curvature of an edge can also be of relevance.

The fact that shearlet-based representations are specifically designed to capture anisotropic structures makes them perfect candidates for the extraction and analysis of edges and ridges. One of the first successful approaches to shearlet-based edge detection was made by Yi et al. [YLEK] who derived a multi-scale algorithm for obtaining both locations and orientations of edges by analyzing the local decay behavior of shearlet coefficients. The theory developed in this work was later extended to the case of shearlet transforms based on compactly supported generators by Kutyniok and Petersen [KP].

Another approach that utilizes complex-valued shearlets and that can be applied to the detection and analysis of both edges and ridges was only recently developed by Reisenhofer and King. In collaboration with the Institute of Thermodynamics at the University of Bremen, this algorithm was already successfully applied to the detection and analysis of flame fronts in recordings of combustion processes [RKK].

External Links

Selected Papers

Inpainting

Inpainting is the task of filling in missing parts of an image with the goal of restoring the original as close as possible. It is a widespread problem in image processing and there are different approaches to its solution. One promising approach is to promote sparsity in the resulting image by thresholding or minimizing the norm of its representation in a fitting dictionary. Due to their optimally sparse approximation of cartoon-like images shearlets are well-suited for the use in such dictionaries.

In recent works theoretical guarantees on the performance of sparsity-seeking inpainting with shearlets have been established. In particular, shearlets were shown to be more useful than wavelets for this task. Moreover, shearlet-based methods performed very well in various numerical tests, also in comparison to other state-of-the-art algorithms.  As a specific application, the inpainting of seismic data has been studied.

Selected Papers

Image Separation

Images often contain two classes of components that differ distinclty in their morphological structure such as point-like and curve-like features. In many applications it is necessary to seperate these features, e.g. in medical imaging when analyzing neurons, which are composed of splines and dendrites. Although this problem is highly underdetermined recent methods from applied harmonic analysis have reached convincing results. The basic approach is to express the mixed image in two different representation systems where each one provides a sparse approximation of one class of features but both are incoherent to each other. Then, usually by thresholding or l1-optimization, a sparse representation in the combined system is found.

Shearlet or curvelet systems, which were specifically constrcuted to represent anisotopic data efficiently, in combination with wavelet systems, which represent point-like singularities well, are a natural choice for this task. Their effectiveness has been confirmed by theoretical results as well as numerical experiments. In theoretical work on this topic the notion of cluster coherence, which measures the geometric clustering of significant coefficients, is essential.

Selected Papers

 

Image Denoising

Denoising is a classical and highly relevant task in image processing. The various methods used for its solution involve different fields of mathematics such as statistics, PDEs and applied harmonic analysis. The approach from applied harmonic analysis utilizes the fact that the coefficients of noise in representation systems such as wavelet, curvelet or shearlet systems are quite evenly distributed whereas the features of the actual picture are preserved in few significant coefficients. By simply thresholding the coeffiecients of the signal in the transformed realm and then applying the inverse transform the signal can thus be denoised. However, this method tends to produce artifacts around sharp discontinuities. To overcome this problem, shearlets are used in more sophisticated algorithms that e.g. involve total variation or diffusion methods.

Selected Papers

 

Image Interpolating

Digital images are often viewed on devices with varying display sizes and therefore have to be rescaled for proper viewing. The process of creating a high-resolution image from a low-resolution image is referred to as image interpolation, upscaling or upsampling. A major challenge of this problem is to avoid blurring of sharp edges. An approach from applied harmonic analysis aims to overcome this by utilizing the sparse representation of such curve-like singularities in shearlet systems. First, a blurred high-resolution estimate is constructed with conventional methods and sparsified by thresholding in the shearlet realm. Then the estimate is refined by high-frequency details from the sparsified version. This approach performed well in numerical experiments.

Selected Papers

 

Generalized Sampling

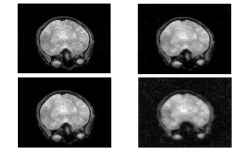
In some medical imaging applications, e.g. MRI, signals have to be recovered from a finite set of measurements. The method of taking those measurements, and thus the representation system used to model this process, is usually mostly fixed. However, the reconstruction system can be chosen freely. By using extra information about the signal to chose the system carfeully the reconstruction can be optimized. If the sizes of the sampling and reconstructing systems are allowed to vary independently of each other the setting is called Generalized Sampling.

Fourier sampling systems and a reconstruction system of compactly supported shearlets have been shown to allow for a stable reconstruction. Moreover, their quotient, the so called stable sampling rate, is almost linear. The proposed method using shearlets outperformed the wavelet approach and a simple Fourier inversion in numerical tests with MRI data.

Selected Papers

 

Inverse Scattering

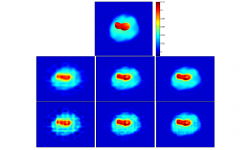
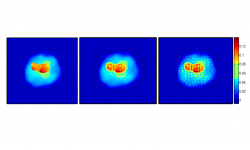
When waves are transmitted through a medium and reach inhomogeneities they are scattered. The inverse scattering problem aims to determine characteristics of these inhomogeneities, e.g. density and shape, from information about the scattered waves. This is used in applications such as echolocation or ultrasound tomography. The inverse scattering problem is again a heavily undetermined problem. However, in many cases the assumption that the scatterer can be modelled as a cartoon-like function is justified. Then, by using its sparse shearlet representation, efficient and precise algorithms for a recovery can be found. This sparsity-seeking approach is applied to two commom methods for solving nonlinear inverse scattering problems: Using a fix-point interation scheme where many linear inverse scattering problems are solved (Born approximation) and optimizing the associated Tykhonov functional.

Selected Papers

 

Digital Watermarking

Digital images can be reproduced and distributed very easily. This makes it hard to determine their authenticity or the ownership of their copyright. One method to solve this problem is to mark the image with a so called digital watermark before distribution. In order to preserve the value of the image, the watermark should not change the visual appearance of the image notably. However, there also must be a reverse algorithm to extract the watermark again. Additionally, the marking should be robust against modifications, also called attacks, of the watermarked image. Such attacks include lossy compression, cropping, adding noise or histogram equalization.

Methods that do not add the watermark directly into the picture but rather manipulate its representation in a well-suited dictionary generally perform well, especially in regard to the appearance of the watermarked image. Wavelet-based algorithms, e.g. as proposed in [WSK] or [BBP], have been established as a standard method of this kind.  Following this idea and motivated by their optimal approximation results for a large class of two-dimensional images, shearlet representation systems have been succesfully introduced to these algorithms in recent years ([ARKB], [MC], [HTHR]).

Selected Papers