Edge Analysis
Inpainting
Image Separation
Image Interpolation
Inverse Scattering
Fourier Sampling

Edge Analysis

The location of edges in images and their geometric properties can contain valuable information about the depicted object. Several algorithms are available that use the anisotropic nature of shearlets to obtain this information.

Inpainting

Shearlet-based algorithms can be used to inpaint missing data blocks in images. In particular, the recovery of seismic data has been studied and tested.

Image Separation

When analyzing visual data it is often necessary to extract certain features from an image. A combination of wavelet and shearlet representation systems can be used to separate point-like and wave-like structures of an image, e.g. the spines and dendrites of a neuron.

Image Interpolation

Images that have been enlarged beyond their original size often show blurring of formerly sharp edges. Adding high-frequence details from sparsified shearlet representations of the original image can help to refine such features.

Inverse Scattering

In echolocation or ultrasound tomography the structure of a medium has to be recovered from information about scattered waves. Sparse shearlet representations of the often cartoon-like scatterer allow for efficient algorithms to solve this problem.

Fourier Sampling

Signals often have to be recovered from a finite set of measurements, e.g. in medical imaging methods such as MRI. The use of compactly supported shearlets for reconstruction can reduce the number of necessary measurements for a given precision.

Welcome to shearlab.org

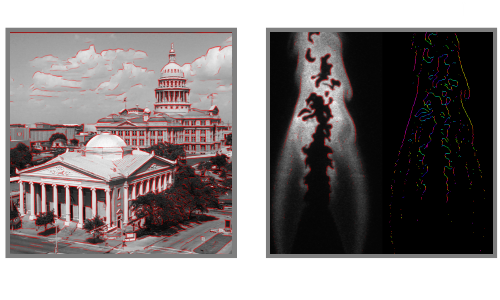
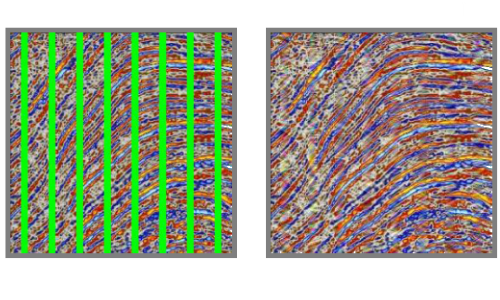
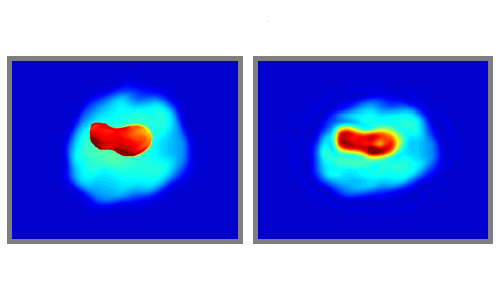
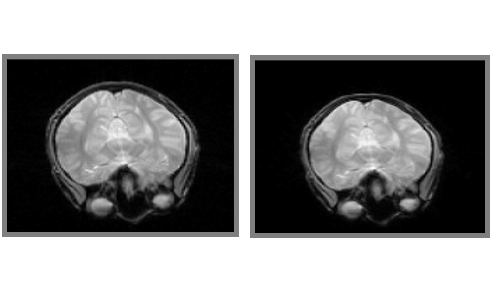
ShearLab is a MATLAB library developed for processing two- and threedimensional data with a certain class of basis functions named shearlets. Such shearlet systems are particularly well adapted to represent anisotropic features (such as curves) that are often crucial in multidimensional data. The resulting representation has proven well-suited for image processing tasks such as inpainting, denoising or image separation. On this website we provide the full MATLAB code, a framework for numerical tests as well as general information on shearlets.

Similiar to wavelet systems, shearlet systems are constructed by modifying generator functions. For wavelet systems, these functions are isotropically scaled and translated. While this is enough to provide an optimally sparse representation for an interesting class of 1D functions it fails to do so in higher dimensions. To compensate this shortcoming, the direction of the generator functions has to be varied. In shearlet theory, this is accomplished by shearing and anisotropic scaling.

Various desirable properties of such shearlet systems have been mathematically proven in recent years. In particular, it has been shown that there are compactly supported generator functions that form a frame for L^2(R^2) and provide optimally sparse representations of cartoon-like functions up to a logarithmic factor. The latter is a key finding in shearlet theory because it is often assumed that most natural signals can in fact be modelled as a cartoon-like function.

However, for a successful application of such a theory a good implementation is necessary. In contrast to rotation, shearing does not disrupt the integer grid and thus makes a unified treatment of the continuous and digital shearlet theory possible. This unity allows for a rather faithful implementation of the digital shearlet transform in MATLAB.

The implementation of ShearLab has been thoroughly tested in various numerical experiments. The detailed results and their analysis can be found in the corresponding publications, the full code for the experiments in the software section.

 

We invite you to explore the site, test the ShearLab library yourself and contact us if you have any questions or remarks!